Cuando los estudiantes de matemáticas de bachillerato o primer curso de universidad hacen integrales, una de las que típicamente les resultan difíciles es la integral de sen(x)*cos(x).
Integración por partes
La integral de sen(x)*cos(x) es una de esas integrales que puedes resolver con el método de integración por partes. No es difícil comenzar a resolverla, pero el problema es que llega un momento en que te encuentras con la misma integral, y entonces a partir de ahí los estudiantes no saben seguir. Vamos a explicar aquí cómo hacer la integral de seno por coseno de x paso a paso.
Lo primero es plantear quién es u y quién es dv en la integración por partes. Bajo la integral que estamos intentando resolver, pongo la famosa forma de resolverla. Elegimos en este caso que u=sen(x) y dv=cos(x). Si esta es la elección, du (derivada de u respecto de x) tiene que ser cos(x)*dx y v (integral de dv) tiene que ser sen(x).
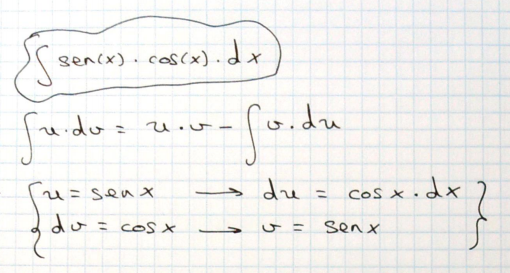
Ahora sustituimos u, v, du y dv en la fórmula, y queda:
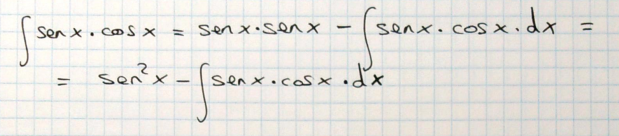
Lo que decía antes: nos ha quedado otra vez una integral sen(x)*cos(x). ¿Qué hacemos? ¿Volvemos a hacer esa integral otra vez por partes? No, porque vamos a llegar a lo mismo, una y otra vez una integral sen(x)*cos(x).
Entonces, ¿qué hacemos? Pues la solución es más sencilla de lo que parece: vamos a agrupar las integrales a un lado de la igualdad y dejar al otro lado el seno cuadrado de x. Es decir, vamos a despejar seno cuadrado de x, pasamos también el 2 al otro lado dividiendo, y listo, ya lo tenemos. No olvides añadir el +C al final, porque estamos haciendo una integral indefinida y tiene infinitas soluciones.

Vale Silvia, pero resulta que yo elegí que u no sea sen(x) sino que u=cos(x), y cuando la hago igual que tú me sale una solución distinta. Venga, ¿lo probamos?

La solución es diferente, porque ya no tenemos un seno cuadrado, sino un coseno cuadrado, y además hay un signo menos. Entonces, ¿qué significa esto? ¿Cómo puede tener una integral dos soluciones distintas?
En realidad las dos soluciones no son diferentes.
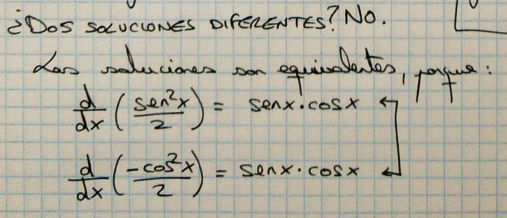
Como puedes ver en la imagen de arriba, si derivamos cualquiera de las dos soluciones, nos da la función primitiva, es decir, la que estábamos intentando integrar, sen(x)*cos(x)




Como evaluó la función, si es una integral definida? Hago la diferencia del inicio y final en el mismo sen^2x/2?
Hola Manuel. Una vez tienes la solución, aplicas la regla de Barrow. Es decir, justo lo que comentas.