A medida que vas teniendo más experiencia en mostrar datos te das cuenta de la importancia que tiene el elegir la mejor manera de representarlos en una gráfica. La escala, los colores, los símbolos que representan los puntos, las curvas de ajuste, las leyendas…. todo tiene que hacerse de la manera más apropiada para que el lector entienda, de un solo vistazo, lo que queremos mostrar.
(Imagen de: Ciencia Activa).
Una vez representados los datos, un problema típico es elegir cuál es la forma de la curva de ajuste a una serie de puntos. Aveces, por simple inspección visual, nos da la impresión de que la nube de puntos se va ajustar muy bien a una recta. En ese caso elegimos un ajuste lineal, calculamos la bondad del ajuste a través de R^2 y si el valor es bueno nos quedamos satisfechos. Sin embargo aveces, aunque nuestra vista y el valor R^2 parezcan confirmarlo, el ajuste lineal no es la respuesta.
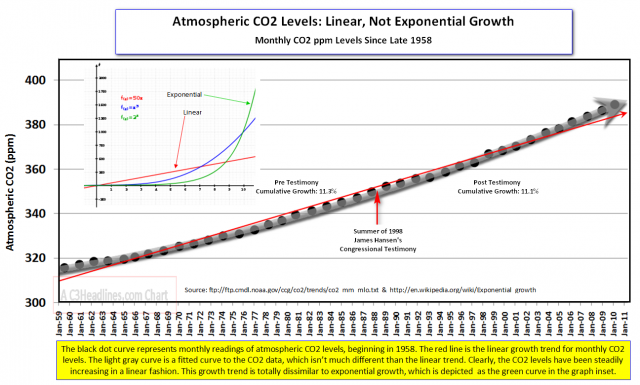
En el blog Topologic Oceans hay un post muy interesante sobre este tema, titulado «Graphing Out Loud: curves and lines«. En este artículo se habla del curioso caso de las series temporales de CO2 claramente manipuladas por el autor del blog C3Headlines en esta entrada. En C3Headlines, un blog que podríamos catalogar facilmente como «negacionista» en asuntos de Cambio Climático, tratan de echar un cable al autor de el todavía más conocido blog negacionista Watts Up With That?, acerca de este artículo donde su autor pone en duda (como siempre), los resultados publicados en un trabajo científico. El trabajo en cuestión es el paper titulado «Evidence for super-exponentially accelerating atmospheric carbon dioxide growth«, de Andreas D. Hüsler y Didier Sornette (Atmospheric and Oceanic Physics, 2011). Hüsler y Sornette llegan a la conclusión de que existe un crecimiento exponencial y acelerado de las concentraciones de CO2 en la atmósfera, pero los blogueros de Watts Up With That? y C3Headlines quieren hacer ver que los expertos no tienen razón y el crecimiento de las concentraciones de CO2 es simplemente lineal. Para ello en C3Headlines lo que hacen es representar los datos de una manera muy dudosa: por un lado, en vez de representar la serie de promedios anuales, eligen representar la serie de promedios de los meses de enero. El por qué solo usan los datos de enero pero en el título de la gráfica no lo aclaran (solo ponen Monthly CO2 ppm levels since late 1958) es todo un misterio que ya nos puede hacer pensar mal (¿quizás los datos de los meses de enero son los que muestran un comportamiento aparentemente más lineal de la serie?).
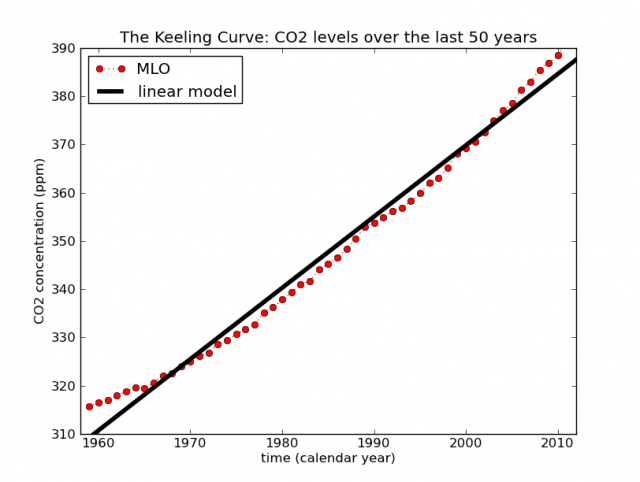
Ahora la cuestión clave es fijarse en el ajuste lineal marcado con una líne roja sobre los puntos grises. En la pequeña gráfica que se incluye en la parte superior izquierda se nos muestra cómo se vería un ajuste lineal (en rojo) y un ajuste exponencial (en verde). A simple vista la serie temporal mostrada parece asemejarse más a la línea roja, luego…el ajuste es lineal. Además, el R^2 es de 0.986, muy bueno, así que ya no hay dudas de que el ajuste lineal es el mejor. Pero, tal y como apunta el autor de Topologic Oceans, hay un pequeño problema: si respresentas la serie con un rango de valores menor en el eje Y, puedes ver que el ajuste lineal está subestimando los valores en los extremos de la gráfica, y sobreestimando en el centro. La gráfica está curvada hacia arriba, es decir, no es lineal. En la figura de arriba ya podía apreciarse esto, pero en esta nueva figura se ve más claro.
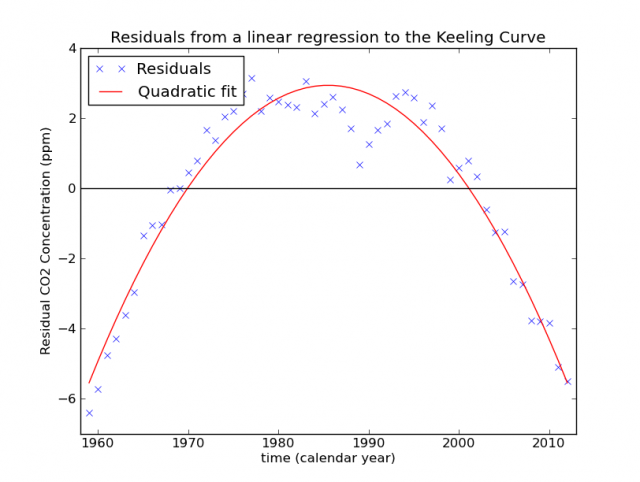
La cuestión es que una regresión lineal va a ajustar una línea de tendencia a cualquier conjunto de datos, sea una distribución de datos lineal o no. Aunque el R^2 sea tan bueno como en este caso, 0.986, esto no significa que el crecimiento del CO2 según esta serie de datos sea lineal. Una buena manera de verlo es calcular los residuos: tenemos una ecuación que describe los datos y podemos restar esa ecuación a los datos para obtener los residuos. Como estamos calculando el modelo con una ecuación lineal, los residuos son, por definición, no lineales. No es que no esperemos residuos si el fenómeno modelizado fuese realmente lineal, sino que los datos en la vida real son ruidosos. Esperamos encontrar variaciones que un modelo lineal no puede tener en cuenta. Si la única componente no lineal de los datos fuese ruido, esa componente obviamente debería tener un aspecto muy ruidoso. Sin embargo, cuando representamos los residuos en el caso de estudio (siguiente figura) vemos que no parecen ruidosos.
Lo que vemos es una clara prueba de que estábamos en lo cierto afirmando que nuestras serie temporal de concentraciones de CO2 mostraban cierta curvatura. De hecho, la curvatura es estadísticamente significativa (p-value ~10^-16 para el ajuste cuadrático).
Bien, pues vamos a buscar entonces el mejor ajuste a nuestros datos. Podemos combinar el modelo de residuos (cuadrático) con el ajuste lineal original, y así tendremos una mejor descripción de los datos. Por un lado tenemos:
Residuos = Ajuste lineal – Datos
y como tenemos un modelo cuadrático para los residuos:
Ajuste cuadrático = Ajuste lineal – Datos
podemos construir un modelo no lineal para nuestros datos:
Modelo no lineal = Ajsute lineal – Ajuste cuadrático
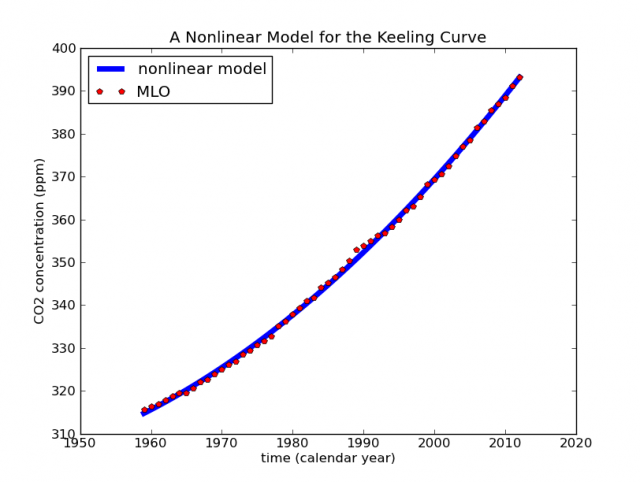
Haciendo esto obtenemos la ecuación de una curva que describe nuestros datos mucho mejor que la regresión lineal inicial:
La curva de ajuste azul ahora se parece bastante a la curva gris que unía los puntos en la primera gráfica. Da la sensación de que en el blog C3 Headlines usaron un modelo no lineal para generar esa curva, pero luego abandonan la idea del modelo no lineal y se empeñan en ajustarlo todo a una recta. Curioso.
Por lo tanto, hemos visto que la serie temporal de CO2 tiene una curvatura significativa que podemos describir con un modelo de polinomio de segundo grado:
Y = a*X^0 + b*X^1 + c*X^2
Este modelo cuadrático es consistente con un modelo exponencial, ya que una función exponencial es solo una parte de un polinomio de grado infinito. Si los datos son exponenciales, nuestro modelo cuadrático está descrito por los primeros términos del polinomio de grado infinito:
e^X = a*X^0 + b*X^1 + c*X^2 + d*X^3 + … + an*X^n + …
Tal y como indica Charlie Soeder en Topologic Oceans, distinguir entre un crecimiento cuadrático, exponencial o superexponencial (que es como describen Hüsler y Didier al crecimiento de la serie de CO2 estudiada en su trabajo) es más complicado y requiere de técnicas estadísticas complicadas que estos autores describen en su paper. Sin embargo sí que es fácil, como hemos visto aquí, desmontar que los datos no son lineales. En todo caso, ya era de esperar encontrar un crecimiento no lineal, simplemente porque un aumento lineal del CO2 tendría que estar caracterizado por una tasa de cambio constante, cosa que no está ocurriendo en la realidad.




I am glad that you enjoyed my article, and I thank you for reposting it!
Me alegro de que haya disfrutado de mi artículo, y doy las gracias por volver a publicar eso!
Charlie, many thanks for your comment. Your blog is so interesting and I will follow it. Thanks!
http://francisthemulenews.wordpress.com/2011/12/21/atencion-pregunta-que-representacion-de-datos-te-parece-mas-adecuada/