Mi blog personal sobre investigación, divulgación científica y música
Etiqueta: gráficas
el pasado día 11 de junio el primer mensaje en que vi en Twitter hizo que me despertara rápido. Era un mensaje de un conocido broker y deportista español que escribe libros y da muchas charlas (seguro que ya sabes quién es 🙂 ) en el que decía «Incremento de la venta de viviendas, volvemos ya a niveles de 2010», y compartía esta imagen.
Llevo unos días tratando de resolver un problema aparentemente muy tonto en una gráfica hecha con MATLAB, pero por mucho que he estado buscando en la ayuda del programa y en internet, no daba con la solución. El problema es el siguiente: representas una serie de datos en una gráfica y añades a la gráfica una leyenda, pero quieres que los símbolos de las leyendas aparezcan en un tamaño más grande que el que tienen por defecto. Parece una tontería, pero por lo visto MATLAB no permite modificar el tamaño de los símbolos de la leyenda de una forma tan intuitiva como lo permite hacer para los símbolos en la propia gráfica.
Voy a poner un ejemplo visual. Esta es una gráfica del tipo scatterm, es decir, una serie de puntos localizados en las coordenadas x e y a los que les asignamos un valores. El dimátero del círculo varía con ese valor.
La interface gráfica de Veusz es sencilla, yo diría que más intuitiva que la de Grapher. Con este programa se pueden hacer muchísimos tipos de gráficas, e incluso anidarlas para formar figuras con varias gráficas en ellas. En la web de Veusz hay muchos ejemplos, con su fichero incluido, de manera que puedes cargarlos en tu ordenador y usarlos como plantilla. Se puede usar además por línea de comandos, usando scripts y como módulo de representación gráfica para Python.
Seguramente habrá otros programas de representación gráfica más sencillos, o con más opciones, pero si buscas un programa gratis, multiplataforma y que respete los NaN en la gráfica, este es el tuyo.
A medida que vas teniendo más experiencia en mostrar datos te das cuenta de la importancia que tiene el elegir la mejor manera de representarlos en una gráfica. La escala, los colores, los símbolos que representan los puntos, las curvas de ajuste, las leyendas…. todo tiene que hacerse de la manera más apropiada para que el lector entienda, de un solo vistazo, lo que queremos mostrar.
(Imagen de: Ciencia Activa).
Una vez representados los datos, un problema típico es elegir cuál es la forma de la curva de ajuste a una serie de puntos. Aveces, por simple inspección visual, nos da la impresión de que la nube de puntos se va ajustar muy bien a una recta. En ese caso elegimos un ajuste lineal, calculamos la bondad del ajuste a través de R^2 y si el valor es bueno nos quedamos satisfechos. Sin embargo aveces, aunque nuestra vista y el valor R^2 parezcan confirmarlo, el ajuste lineal no es la respuesta.
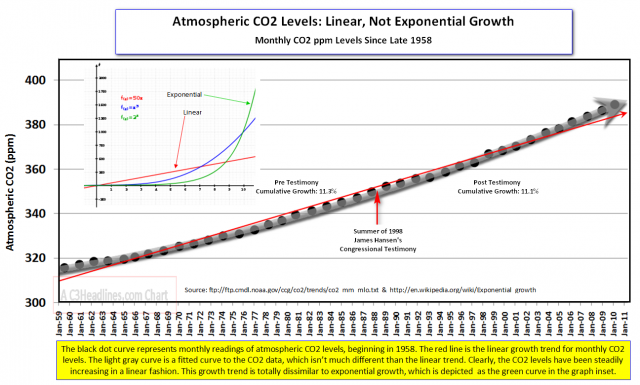
En el blog Topologic Oceans hay un post muy interesante sobre este tema, titulado «Graphing Out Loud: curves and lines«. En este artículo se habla del curioso caso de las series temporales de CO2 claramente manipuladas por el autor del blog C3Headlines en esta entrada. En C3Headlines, un blog que podríamos catalogar facilmente como «negacionista» en asuntos de Cambio Climático, tratan de echar un cable al autor de el todavía más conocido blog negacionista Watts Up With That?, acerca de este artículo donde su autor pone en duda (como siempre), los resultados publicados en un trabajo científico. El trabajo en cuestión es el paper titulado «Evidence for super-exponentially accelerating atmospheric carbon dioxide growth«, de Andreas D. Hüsler y Didier Sornette (Atmospheric and Oceanic Physics, 2011). Hüsler y Sornette llegan a la conclusión de que existe un crecimiento exponencial y acelerado de las concentraciones de CO2 en la atmósfera, pero los blogueros de Watts Up With That? y C3Headlines quieren hacer ver que los expertos no tienen razón y el crecimiento de las concentraciones de CO2 es simplemente lineal. Para ello en C3Headlines lo que hacen es representar los datos de una manera muy dudosa: por un lado, en vez de representar la serie de promedios anuales, eligen representar la serie de promedios de los meses de enero. El por qué solo usan los datos de enero pero en el título de la gráfica no lo aclaran (solo ponen Monthly CO2 ppm levels since late 1958) es todo un misterio que ya nos puede hacer pensar mal (¿quizás los datos de los meses de enero son los que muestran un comportamiento aparentemente más lineal de la serie?).
Ahora la cuestión clave es fijarse en el ajuste lineal marcado con una líne roja sobre los puntos grises. En la pequeña gráfica que se incluye en la parte superior izquierda se nos muestra cómo se vería un ajuste lineal (en rojo) y un ajuste exponencial (en verde). A simple vista la serie temporal mostrada parece asemejarse más a la línea roja, luego…el ajuste es lineal. Además, el R^2 es de 0.986, muy bueno, así que ya no hay dudas de que el ajuste lineal es el mejor. Pero, tal y como apunta el autor de Topologic Oceans, hay un pequeño problema